10th Maths - Book Back Answers - Chapter 3 Exercise 3.12 - English Medium Guides

  

 

SSLC / 10th - Maths - Book Back Answers - Chapter 3 Exercise 3.12 - English Medium

Tamil Nadu Board 10th Standard Maths - Chapter 3 Exercise 3.12: Book Back Answers and Solutions

    This post covers the book back answers and solutions for Chapter 3 Exercise 3.12 – Maths from the Tamil Nadu State Board 10th Standard textbook. These detailed answers have been carefully prepared by our expert teachers at KalviTips.com.

    We have explained each answer in a simple, easy-to-understand format, highlighting important points step by step under the relevant subtopics. Students are advised to read and memorize these subtopics thoroughly. Once you understand the main concepts, you’ll be able to connect other related points with real-life examples and confidently present them in your tests and exams.

    By going through this material, you’ll gain a strong understanding of Chapter 3 Exercise 3.12 along with the corresponding book back questions and answers (PDF format).

Question Types Covered:

• 1 Mark Questions: Choose the correct answer, Fill in the blanks, Identify the correct statement, Match the following 
• 2 Mark Questions: Answer briefly 
• 3, 4, and 5 Mark Questions: Answer in detail

All answers are presented in a clear and student-friendly manner, focusing on key points to help you score full marks.

All the best, Class 10 students! Prepare well and aim for top scores. Thank you!

Chapter 3 Algebra Ex 3.12

1. If the difference between a number and its reciprocal is $\frac{24}{5}$, find the number.

Answer Key:
Let the number be “x” and its reciprocal is $\frac{1}{x}$
By the given condition
$x-\frac{1}{x}=\frac{24}{5}$
$\frac{x^2-1}{x}=\frac{24}{5}$
5x² – 5 = 24x
5x² – 24x – 5 = 0

5x² – 25x + x – 5 = 0 ⇒ 5x (x – 5) + 1(x – 5) = 0

(x – 5) (5x – 1) = 0 ⇒ x – 5 = 0 or 5x + 1 = 0
x = 5 or 5x = -1 ⇒ x = $\frac{-1}{5}$
The number is 5 or $\frac{-1}{5}$

 

2. A garden measuring 12m by 16m is to have a pedestrian pathway that is meters wide installed all the way around so that it increases the total area to 285 m². What is the width of the pathway?
Answer Key:

Let the width of the rectangle be “ω”
Length of the outer rectangle = 16 + (ω + ω)
16 + 2ω
Breadth of the outer rectangle = 12 + 2ω

By the given condition
(16 + 2ω) (12 + 2ω) = 285
192 + 32 ω + 24 ω + 4 ω² = 285
4 ω² + 56ω = 285 – 192
4 ω² + 56 ω = 93
4 ω²+ 56 ω – 93 = 0
Here a = 4, b = 56, c = -93

 = 1.5 or -15.5 (Width is not negative)
∴ Width of the path way = 1.5 m

 

3. A bus covers a distance of 90 km at a uniform speed. Had the speed been 15 km/hour more it would have taken 30 minutes less for the journey. Find the original speed of the journey.
Answer Key:
Let the original speed of the bus be “x” km/hr
Time taken to cover 90 km = $\frac{90}{x}$
After increasing the speed by 15 km/hr
Time taken to cover 90 km = $\frac{90}{x+15}$
By the given condition
$\frac{90}{x}-\frac{90}{x+15}=\frac{1}{2}$
$\frac{90(x+15)-90x}{(x+15)}=\frac{1}{2}$
90x + 1350 – 90x = $\frac{x^2+15x}{2}$
1350 =$\frac{x^2+15x}{2}$
2700 = x² + 15x

x² + 15x – 2700 = 0
(x + 60) (x – 45) = 0
x + 60 = 0 or x – 45 = 0
x = – 60 or x = 45
The speed will not be negative
∴ Original speed of the bus = 45 km/hr

 

4. A girl is twice as old as her sister. Five years hence, the product of their ages – (in years) will be 375. Find their present ages.
Answer Key:
Let the age of the sister be “x”
The age of the girl = 2x
Five years hence
Age of the sister = x + 5
Age of the girl = 2x + 5
By the given condition
(x + 5) (2x + 5) = 375
2x² + 5x + 10x + 25 = 375
2x² + 15x – 350 = 0
a = 2, b = 15, c = -350

Age will not be negative
Age of the girl = 10 years
Age of the sister = 20 years (2 × 10)

 

5. A pole has to be erected at a point on the boundary of a circular ground of diameter 20 m in such a way that the difference of its distances from two diametricallyopposite fixed gates P and Q on the boundary is 4 m. Is it possible to do so? If Answer KeyKeyis yes at what distance from the two gates should the pole be erected?
Answer Key:
Let “R” be the required location of the pole
Let the distance from the gate P is “x” m : PR = “x” m
The distance from the gate Q is (x + 4)m
∴ QR = (x + 4)m
In the right ∆ PQR,

PR² + QR² = PQ² (By Pythagoras theorem)
x² + (x + 4)² = 20²
x² + x² + 16 + 8x = 400
2x² + 8x – 384 = 0

x² + 4x – 192 = 0(divided by 2)
(x + 16) (x – 12) = 0
x + 16 = 0 or x – 12 = 0 [negative value is not considered]
x = -16 or x = 12
Yes it is possible to erect
The distance from the two gates are 12 m and 16 m

 

6. From a group of 2x² black bees , square root of half of the group went to a tree. Again eight-ninth of the bees went to the same tree. The remaining two got caught up in a fragrant lotus. How many bees were there in total?
Answer Key:

Total numbers of black bees = 2x²
Half of the group = $\frac{1}{2}$ × 2x² = x²
Square root of half of the group = $\sqrt{x^2}$ = x
Eight – ninth of the bees = $\frac{8}{9}\times 2x^2=\frac{16x^2}{9}$
Number ofbees in the lotus = 2
By the given condition
x +$\frac{16x^2}{9}$ + 2 = 2x²
(Multiply by 9) 9x + 16×2 + 18 = 18x²

18x² – 16x² – 9x – 18 = 0 ⇒ 2x² – 9x – 18 = 0
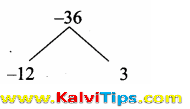
2x² – 12x + 3x – 18 = 0
2x(x – 6) + 3 (x – 6) = 0
(x – 6) (2x + 3) = 0
x – 6 = 0 or 2x + 3 = 0
x = 6 or 2x = -3 ⇒ x = $\frac{-3}{2}$ (number of bees will not be negative)
Total number of black bees = 2x² = 2(6)²
= 72

 

7. Music is been played in two opposite galleries with certain group of people. In the first gallery a group of 4 singers were singing and in the second gallery 9 singers were singing. The two galleries are separated by the distance of 70 m. Where should a person stand for hearing the same intensity of the singers voice?
(Hint: The ratio of the sound intensity is equal to the square of the ratio of their corresponding distances).
Answer Key: 

Number of singers in the first group = 4
Number of singers in the second group = 9
Distance between the two galleries = 70 m
Let the distance of the person from the first group be x
and the distance of the person from the second group be 70 – x
By the given condition
4 : 9 = x² : (70 – x)² (by the given hint)
$\frac{4}{9}=\frac{x^2}{(70-x{)}^2}$
$\frac{2}{3}=\frac{x}{70-x}$ [taking square root on both sides]
3x = 140 – 2x
5x = 140
x = $\frac{140}{5}$ = 28
The required distance to hear same intensity of the singers voice from the first galleries is 28m
The required distance to hear same intensity of the singers voice from the second galleries is (70 – 28) = 42 m

 

8. There is a square field whose side is 10 m. A square flower bed is prepared in its centre leaving a gravel path all round the flower bed. The total cost of laying the flower bed and gravelling the path at ₹3 and ₹4 per square metre respectively is ₹364. Find the width of the gravel path.
Answer Key:
Let the width of the gravel path be ‘x’
Side of the flower bed = 10 – (x + x)
= 10 – 2x

 Area of the path way = Area of the field – Area of the flower bed
= 10 × 10 – (10 – 2x) (10 – 2x) sq.m
= 100 – (100 + 4x² – 40x)
= 100 – 100 – 4x² + 40x
= 40x – 4x² sq.m
Area of the flower bed = (10 – 2x) (10 – 2x) sq.m.
= 100 + 4x² – 40x
By the given condition

3(100 + 4x² – 40x) + 4(40x – 4x²) = 364
300 + 12x² – 120x + 160x – 16x² = 364
-4x² + 40x + 300 – 364 = 0
-4x² + 40x – 64 = 0
(÷ by 4) ⇒ x² – 10x + 16 = 0
[The width must not be equal to 8 m since the side of the field is 10m]
(x – 8) (x – 2) = 0
x – 8 = 0 or x – 2 = 0 x = 8 or x = 2
Width of the gravel path = 2 m

 

9. The hypotenuse of a right angled triangle is 25 cm and its perimeter 56 cm. Find the length of the smallest side.
Answer Key:
Perimeter of a right angle triangle = 56 cm
Sum of the two sides + hypotenuse = 56
Sum of the two sides = 56 – 25
= 31 cm
Let one side of the triangle be “x”

The other side of the triangle = (31 – x) cm
By Pythagoras theorem
AB² + BC² = AC²
x² + (31 – x)² = 25²
x² + 961 + x² – 62x = 625

2x² – 62x + 961 – 625 = 0
2x² – 62x + 336 = 0 ⇒ x² – 31x + 168 = 0
(x – 24) (x – 7) = 0
x – 24 = 0 (or) x – 7 = 0
x = 24 (or) x = 7
Length of the smallest side is 7 cm