Tamil Nadu Board 10th Standard Maths - Chapter 2 Exercise 2.2: Book Back Answers and Solutions
This post covers the book back answers and solutions for Chapter 2 Exercise 2.2 – Maths from the Tamil Nadu State Board 10th Standard Maths textbook. These detailed answers have been carefully prepared by our expert teachers at KalviTips.com.
We have explained each answer in a simple, easy-to-understand format, highlighting important points step by step under the relevant subtopics. Students are advised to read and memorize these subtopics thoroughly. Once you understand the main concepts, you’ll be able to connect other related points with real-life examples and confidently present them in your tests and exams.
By going through this material, you’ll gain a strong understanding of Chapter 2 Exercise 2.2 along with the corresponding book back questions and answers (PDF format).
Question Types Covered:
- 1 Mark Questions: Choose the correct answer, Fill in the blanks, Identify the correct statement, Match the following
- 2 Mark Questions: Answer briefly
- 3, 4, and 5 Mark Questions: Answer in detail
All answers are presented in a clear and student-friendly manner, focusing on key points to help you score full marks.
All the best, Class 10 students! Prepare well and aim for top scores. Thank you!
Chapter 2 Numbers and Sequences Ex 2.2
Answer Key:
4n = (22)n = 22n
= 2n × 2n
2 is a factor of 4n
∴ 4n is always even.
Answer Key:
2n × 5m
2n is always even for all values of n.
5m is always odd and ends with 5 for all values of m.
But 2n × 5m is always even and ends in 0.
∴ 2n × 5m cannot end with the digit 5 for any values of m. No value of m will satisfy 2n × 5m ends in 5.
Answer Key:
To find the HCF of 252525 and 363636 by using Euclid’s Division algorithm.
363636 = 252525 × 1 + 111111
The remainder 111111 ≠ 0
By division of Euclid’s algorithm
252525 = 111111 × 2 + 30303
The remainder 30303 ≠ 0
Again by division of Euclid’s algorithm
111111 = 30303 × 3 + 20202
The remainder 20202 ≠ 0
Again by division of Euclid’s algorithm.
30303 = 20202 + 10101
The remainder 10101 ≠ 0
Again by division of Euclid’s algorithm.
20202 = 10101 × 2 + 0
The remainder is 0
∴ The H.C.F. is 10101
Answer Key:
Using factor tree method factorise 13824

.PNG)
Answer Key:
Given 113400 = p1x1 × p2x2 × p3x3 × p4x4
Using tree method factorize 113400
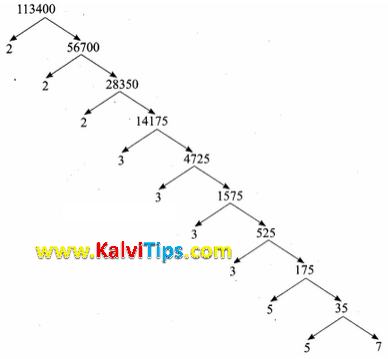
Answer Key:
Factorise 408 and 170 by factor tree method

Answer Key:
The greatest number of 6 digits is 999999.
The greatest number must be divisible by L.C.M. of 24, 15 and 36
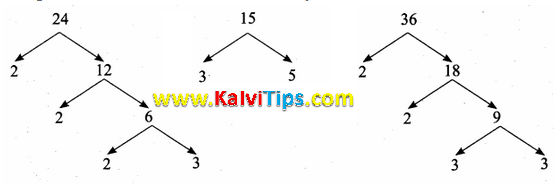
.PNG)
Answer Key:
Answer Key:
Find the L.C.M of first 10 natural numbers.









0 Comments:
Post a Comment