10th Maths - Book Back Answers - Chapter 4 Unit Exercise 4.4 - English Medium Guides

 

SSLC / 10th - Maths - Book Back Answers - Chapter 4 Unit Excercise 4.4 - English Medium

Tamil Nadu Board 10th Standard Maths - Chapter 4 Unit Exercise 4.4: Book Back Answers and Solutions

    This post covers the book back answers and solutions for Chapter 4 Unit Exercise 4.4 – Maths from the Tamil Nadu State Board 10th Standard textbook. These detailed answers have been carefully prepared by our expert teachers at KalviTips.com.

    We have explained each answer in a simple, easy-to-understand format, highlighting important points step by step under the relevant subtopics. Students are advised to read and memorize these subtopics thoroughly. Once you understand the main concepts, you’ll be able to connect other related points with real-life examples and confidently present them in your tests and exams.

    By going through this material, you’ll gain a strong understanding of Chapter 4 Unit Exercise 4.4 along with the corresponding book back questions and answers (PDF format).

Question Types Covered:

• 1 Mark Questions: Choose the correct answer, Fill in the blanks, Identify the correct statement, Match the following 
• 2 Mark Questions: Answer briefly 
• 3, 4, and 5 Mark Questions: Answer in detail

All answers are presented in a clear and student-friendly manner, focusing on key points to help you score full marks.

All the best, Class 10 students! Prepare well and aim for top scores. Thank you!

Chapter 4 Algebra Unit Ex 4.4

1. The length of the tangent to a circle from a point P, which is 25 cm away from the centre is 24 cm. What is the radius of the circle?
Answer Key:
Let the radius AB be r. In the right ∆ ABO,
OB² = OA² + AB²
25² = 24² + r²

25² – 24² = r²
(25 + 24) (25 – 24) = r²
r = $\sqrt{49}$=7
Radius of the circle = 7 cm

 

2. ∆ LMN is a right angled triangle with ∠L = 90°. A circle is inscribed in it. The lengths of the sides containing the right angle are 6 cm and 8 cm. Find the radius of the circle.
Answer Key:

LN = 6; ML = 8. In the right ∆ LMN,
MN² = LN² + LM²
= 6² + 8² = 36 + 64 = 100
MN = $\sqrt{100}$= 10

OA= OB = OC = r
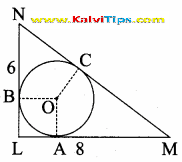
AN = CN (Tangent of the circle)
LN – AL= CN
LN – r = CN
8 – r = CN ……(1)
MC = MB (tangent of the circle)
MC = ML – LB
MC = 6 – r …….(2)

Add (1) and (2)
MC + CN = (6 – r) + (8 – r)
MN = 14 – 2r
10 = 14 – 2r
2r = 14 – 10 = 4
r = $\frac{4}{2}$ = 2 cm
radius of the circle = 2 cm

 

3. A circle is inscribed in ∆ ABC having sides 8 cm, 10 cm and 12 cm as shown in figure, Find AD, BE and CF.

Answer Key:

AD = AF = x (tangent of the circle)
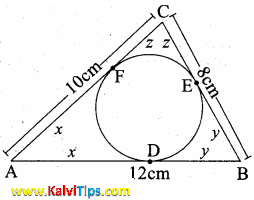
BD = BE = y (tangent of the circle)
CE = CF = z (tangent of the circle)
AB = AD + DB
x + y = 12 ……(1)
BC = BE + EC
y + z= 8 …….(2)
AC = AF + FC
x + z = 10 ……(3)
Add (1) (2) and (3)
2x + 2y + 2z = 12 + 8 + 10
x + y + z = $\frac{30}{2}$ = 15 …….(4)
By x + y = 12 in (4)
z = 3
y + z = 8 in (4)
x = 7
x + z = 10 in (4)
y = 5
AD = 7 cm; BE = 5 cm and CF = 3 cm

 

4. PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120° . Find ∠OPQ.
Answer Key:

∠POQ = 180° – 120° = 60°
In ∆OPQ, we know

∠POQ + ∠OQP + ∠OPQ = 180°
(Sum of the angles of a ∆ is 180°)
60° + 90° + ∠OPQ = 180°
∠OPQ = 180° – 150° = 30°
∠OPQ = 30°

 

5. A tangent ST to a circle touches it at B. AB is a chord such that ∠ABT = 65°. Find ∠AOB, where “O” is the centre of the circle.
Answer Key:
Given ∠ABT = 65°
∠OBT = 90°(TB is the tangent of the circle)
∠ABO = 90° – 65° = 25°
∠ABO + ∠BOA + ∠OAB = 180°
25° + x + 25° = 180° (Sum of the angles of a ∆)

(OA and OB are the radius of the circle.
∴ ∠ABO = ∠BAO = 25°
x + 50 = 180°
x = 180° – 50° = 130°
∴ ∠BOA = 130°

 

6. In figure, O is the centre of the circle with radius 5 cm. T is a point such that OT = 13 cm and OT intersects the circle E, if AB is the tangent to the circle at E, find the length of AB.

Answer Key:

In the right ∆ OTP,
PT² = OT² – OP²
= 13² – 5²
= 169 – 25
= 144
PT = $\sqrt{144}$ = 12 cm
Since lengths of tangent drawn from a point to circle are equal.
∴ AP = AE = x
AT = PT – AP
= (12 – x) cm
Since AB is the tangent to the circle E.
∴ OE ⊥ AB
∠OEA = 90°
∠AET = 90°
In ∆AET, AT² = AE² + ET²
In the right triangle AET,
AT² = AE² + ET²
(12 – x)² = x² + (13 – 5)²
144 – 24x + x² = x² + 64
24x = 80 ⇒ x = $\frac{80}{24}=\frac{20}{6}=\frac{10}{3}$
BE = $\frac{10}{3}$ cm
AB = AE + BE
= $\frac{10}{3}+\frac{10}{3}=\frac{20}{3}$
Lenght of AB = $\frac{20}{3}$ cm

 

7. In two concentric circles, a chord of length 16 cm of larger circle becomes a tangent to the smaller circle whose radius is 6 cm. Find the radius of the larger circle.
Answer Key:
Here AP = PB = 8 cm
In ∆OPA,
OA² = OP² + AP²

= 6² + 8²
= 36 + 64
= 100
OA = $\sqrt{100}$= 10 cm
Radius of the larger circle = 10 cm

 

8. Two circles with centres O and O’ of radii 3 cm and 4 cm, respectively intersect at two points P and Q, such that OP and O’ P are tangents to the two circles. Find the length of the common chord PQ.
Answer Key:
In ∆ OO’P
(O’O)² = OP² + O’P²
= 3² + 4²

= 9 + 16
(OO’)² = 25
∴ OO’ = 5cm
Since the line joining the centres of two intersecting circles is perpendicular bisector of their common chord.
OR ⊥ PQ and PR = RQ
Let OR be x, then O’R = 5 – x again Let PR = RQ = y cm
In ∆ ORP, OP² = OR² + PR²
9 = x² + y² …(1)
In ∆ O’RP, O’P² = O’R² + PR²
16 = (5 – x)² + y²
16 = 25 + x² – 10x + y²
16 = x² + y² + 25 – 10x
16 = 9 + 25 – 10x (from 1)
16 = 34 – 10x
10x = 34 – 16 = 18
x = $\frac{18}{10}$= 1.8 cm
Substitute the value of x = 1.8 in (1)
9 = (1.8)² + y²
y² = 9 – 3.24
y² = 5.76
y = $\sqrt{5.76}$= 2.4 cm
Hence PQ = 2 (2.4) = 4.8 cm
Length of the common chord PQ = 4.8 cm

 

9. Show that the angle bisectors of a triangle are concurrent.
Answer Key:
Given: ABC is a triangle. AD, BE and CF are the angle bisector of ∠A, ∠B, and ∠C.
To Prove: Bisector AD, BE and CF intersect
Proof: The angle bisectors AD and BE meet at O. Assume CF does not pass through O. By angle bisector theorem.
AD is the angle bisector of ∠A
$\frac{BD}{DC}=\frac{AB}{AC}....\left(1\right)$
BE is the angle bisector of ∠B

$\frac{CE}{EA}=\frac{BC}{AB}....\left(2\right)$
CF is the angle bisector ∠C
$\frac{AF}{FB}=\frac{AC}{BC}....\left(3\right)$
Multiply (1) (2) and (3)
$\frac{BD}{DC}\times \frac{CE}{EA}\times \frac{AF}{FB}=\frac{AB}{AC}\times \frac{BC}{AB}\times \frac{AC}{BC}$
So by Ceva’s theorem.
The bisector AD, BE and CF are concurrent.

 

10. In ∆ABC , with ∠B = 90° , BC = 6 cm and AB = 8 cm, D is a point on AC such that AD = 2 cm and E is the midpoint of AB. Join D to E and extend it to meet at F. Find BF.
Answer Key:

Consider ∆ABC. Then D, E and F are respective points on the sides AC, AB and BC.
By construction D, E, F are collinear.
By Menelaus’ theorem $\frac{AE}{EB}\times \frac{BF}{FC}\times \frac{CD}{DA}=1....\left(1\right)$
AD = 2 cm; AE = EB = 4 cm; BC = 6 cm; FC = FB + BC = x + 6
In ∆ABC, By Pythagoras theorem.

AC²= AB² + BC²
AC² = 8² + 6² = 64 + 36 = 100
AC = $\sqrt{100}$= 10
CD = AC – AD
= 10 – 2 = 8 cm
Substituting the values in (1) we get
$\frac{4}{4}\times \frac{\mathrm{x}}{\mathrm{x}+6}\times \frac{8}{2}=1$
$\frac{\mathrm{x}}{\mathrm{x}+6}\times 4=1$
4x = x + 6
3x = 6 ⇒ x =$\frac{6}{3}$ = 2
The value of BF = 2 cm

 

11. An artist has created a triangular stained glass window and has one strip of small length left before completing the window. She needs to figure out the length of left out portion based on the lengths of the other sides as shown in the figure.

Answer Key:

Given that AE = 3 cm, EC = 4 cm, CD = 10 cm, DB = 3 cm, AF = 5 cm.
Let FB be x
Using Ceva’s theorem we have
$\frac{AE}{Ec}\times \frac{CD}{DB}\times \frac{BF}{AF}=1....\left(1\right)$
$\frac{3}{4}\times \frac{10}{3}\times \frac{\mathrm{x}}{5}=1$
$\frac{2\mathrm{x}}{4}=1$
2x = 4 ⇒ x = $\frac{4}{2}$= 2
The value of BF = 2

 

12. Draw a tangent at any point R on the circle of radius 3.4 cm and centre at P ?

Answer Key:
Given Radius = 3.4 cm

Steps of construction:

1. Draw a circle with centre “O” of radius 3.4 cm.
2. Take a point P on the circle Join OP.
3. Draw a perpendicular line TT’ to OP which passes through P.
4. TT’ is the required tangent.

 

13. Draw a circle of radius 4.5 cm. Take a point on the circle. Draw the tangent at that point using the alternate segment theorem.
Answer Key:

Radius of the circle = 4.5 cm

Steps of construction:

1. With O as centre, draw a circle of radius 4.5 cm.
2. Take a point L on the circle. Through L draw any chord LM.
3. Take a point M distinct from L and N on the circle, so that L, M, N are in anti-clockwise direction. Join LN and NM.
4. Through “L” draw tangent TT’such that ∠TLM = ∠MNL
5. TT’ is the required tangent.

 

14. Draw the two tangents from a point which is 10 cm away from the centre of a circle of radius 5 cm. Also, measure the lengths of the tangents.
Answer Key:

Radius = 5 cm; Distance = 10 cm

Steps of construction:

1. With O as centre, draw a circle of radius 5 cm.
2. Draw a line OP =10 cm.
3. Draw a perpendicular bisector of OP, which cuts OP at M.
4. With M as centre and MO as radius draw a circle which cuts previous circle at A and B.
5. Join AP and BP. AP and BP are the required tangents.

 

Verification: In the right ∆ OAP
PA² = OP² – OA²
= 10² – 5² = $\sqrt{100-25}=\sqrt{75}$ = 8.7 cm
Lenght of the tangent is = 8.7 cm

 

15. Take a point which is 11 cm away from the centre of a circle of radius 4 cm and draw the two tangents to the circle from that point.
Answer Key:
Radius = 4 cm; Distance = 11 cm

Steps of construction:

1. With O as centre, draw a circle of radius 4 cm.
2. Draw a line OP = 11 cm.
3. Draw a perpendicular bisector of OP, which cuts OP at M.
4. With M as centre and MO as radius, draw a circle which cuts previous circle A and B.
5. Join AP and BP. AP and BP are the required tangents.

This the length of the tangents PA = PB = 10.2 cm
Verification: In the right angle triangle OAP
PA² = OP² – OA²
= 11² – 4² = 121 – 16 = 105
PA = $\sqrt{105}$ = 10.2 cm
Length of the tangents = 10.2 cm

 

16. Draw the two tangents from a point which is 5 cm away from the centre of a circle of diameter 6 cm. Also, measure the lengths of the tangents.
Answer Key:

Radius = 3cm; Distance = 5cm.

Steps of construction:

1. With O as centre, draw a circle of radius 3 cm.
2. Draw a line OP = 5 cm.
3. Draw a perpendicular bisector of OP, which cuts OP at M.
4. With M as centre and MO as radius draw a circle which cuts previous circles at A and B.
5. Join AP and BP, AP and BP are the required tangents.

The length of the tangent PA = PB = 4 cm
Verification: In the right angle triangle OAP
PA² = OP² – OA²
= 5² – 3²
= 25 – 9
= 16 PA
= $\sqrt{16}$= 4 cm
Length of the tangent = 4 cm

 

17. Draw a tangent to the circle from the point P having radius 3.6 cm, and centre at O. Point P is at a distance 7.2 cm from the centre.
Answer Key:
Radius = 3.6; Distance = 7.2 cm.

Steps of construction:

1. With O as centre, draw a circle of radius 3.6 cm.
2. Draw a line OP = 7.2 cm.
3. Draw a perpendicular bisector of OP which cuts OP at M.
4. With M as centre and MO as radius draw a circle which cuts the previous circle at A and B.
5. Join AP and BP, AP and BP are the required tangents.

Length of the tangents PA = PB = 6.26 cm
Verification: In the right triangle ∆OAP
PA² = OP² – OA²
= 7.22 – 3.62 =(7.2 + 3.6) (7.2 – 3.6)
PA² = 10.8 × 3.6 = $\sqrt{38.88}$
PA = 6.2 cm
Length of the tangent = 6.2 cm