Tamil Nadu Board 10th Standard Maths - Chapter 3 Exercise 3.3: Book Back Answers and Solutions
This post covers the book back answers and solutions for Chapter 3 Exercise 3.3 – Maths from the Tamil Nadu State Board 10th Standard textbook. These detailed answers have been carefully prepared by our expert teachers at KalviTips.com.
We have explained each answer in a simple, easy-to-understand format, highlighting important points step by step under the relevant subtopics. Students are advised to read and memorize these subtopics thoroughly. Once you understand the main concepts, you’ll be able to connect other related points with real-life examples and confidently present them in your tests and exams.
By going through this material, you’ll gain a strong understanding of Chapter 3 Exercise 3.3 along with the corresponding book back questions and answers (PDF format).
Question Types Covered:
- 1 Mark Questions: Choose the correct answer, Fill in the blanks, Identify the correct statement, Match the following
- 2 Mark Questions: Answer briefly
- 3, 4, and 5 Mark Questions: Answer in detail
All answers are presented in a clear and student-friendly manner, focusing on key points to help you score full marks.
All the best, Class 10 students! Prepare well and aim for top scores. Thank you!
Chapter 3 Algebra Ex 3.3
Answer Key:
p(x) = 21 x2y = 3 × 7 × x2 × y
g(x) = 35xy2 = 5 × 7 × x × y2
G.C.D = 7 xy
L.C.M = 3 × 5 × 7 x2 × y2
= 105 x2y2
L.C.M × G.C.D = 105x2y2 × 7xy
= 735 x3y3 ….(1)
p(x) × g(x) = 21x2y × 35xy2
= 735x3y3 ….(2)
From (1) and (2) we get
L.C.M × G.C.D. = p(x) × g(x)
Answer Key:
p(x) = (x3 – 1) (x + 1) = (x – 1) (x2 + x + 1) (x + 1)
g(x) = x3 + 1 = (x + 1) (x2 – x + 1)
G.C.D = (x + 1)
L.C.M = (x + 1) (x – 1) (x2 + x + 1) (x2 – x + 1)
L.C.M × G.C.D = (x + 1) (x – 1)(x2 + x + 1)(x2 – x + 1)x(x + 1)
= (x + 1)2 (x – 1) (x2 + x + 1) (x2 – x + 1) ……….(1)
p(x) × g(x) = (x – 1) (x2 + x + 1) (x + 1) (x + 1) (x2 – x + 1)
= (x + 1)2 (x – 1) (x2 + x + 1) (x2 – x + 1) ……….(2)
From (1) and (2) we get
L.C.M × G.C.D. = p(x) × g(x)
Answer Key:
g(x) = x2 + xy = x(x + y)
G.C.D = x(x+y)
L.C.M = xy (x +y).
L.C.M × G.C.D = xy(x + y) × x(x + y)
= x2y(x + y)2 …..(1)
p(x) × g(x) = xy(x + y) × x(x + y)
= x2y(x + y)2
From (1) and (2) we get
L.C.M × G.C.D. = p(x) × g(x)
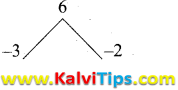
(i) a2 + 4a – 12, a2 – 5a + 6 whose GCD is a – 2
Answer Key:
p(x) = a2 + 4a – 12
= a (a + 6) – 2(a + 6)
= (a + 6) (a – 2)

= a2 – 3a – 2a + 6
%20-%20English%20Medium%20Guides.png)
= (a – 3) (a – 2)
%20-%20English%20Medium%20Guides.png)
Answer Key:
p(x) = x4 – 27a3x = x[x3 – 27a3]
= x[x3 – (3a)3]
= x(x – 3a) (x2 + 3ax + 9a2)
g(x) = (x – 3a)2
G.C.D. = x – 3a
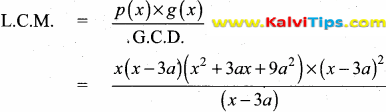%20-%20English%20Medium%20Guides.png)
(i) 12(x4 – x3), 8(x4 – 3x3 + 2x2) whose LCM is 24x3 (x – 1)(x – 2)
Answer Key:
p(x) = 12(x4 – x3)
= 12x3(x- 1)
g(x) = 8(x4 – 3x3 + 2x2)
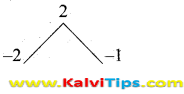
= 8x2(x – 2)(x – 1)
L.C.M. = 24x3 (x – 1) (x – 2)
%20-%20English%20Medium%20Guides.png)
Answer Key:
p(x) = x3 + y3
= (x + y)(x2 – xy + y2)
g(x) = x4 + x2y2 + y4 = [x2 + y2]2 – (xy)2
= (x2 + y2 + xy) (x2 + y2 – xy)
L.C.M. = (x3 + y3) (x2 + xy + y2)
(x + y) (x2 – xy + y2) (x2 + xy + y2)
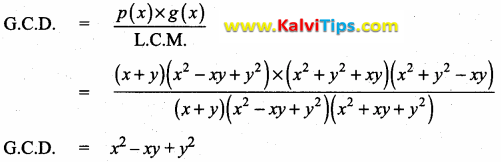%20-%20English%20Medium%20Guides.png)
 Answer Key:
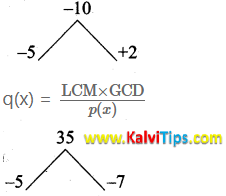
Answer Key:= (a – 7) (a2 – 3a – 10)
= (a – 7) (a – 5) (a + 2)

p(x) = a2 -12a + 35
= (a – 5)(a – 7)
%20-%20English%20Medium%20Guides.png)
(x2 + y2)[(x2 + y2)2-(xy)2]
(x2 + y2) (x2 + y2 + xy) (x2 + y2 – xy)
G.C.D. = x2 – y2
(x + y)(x – y)
q(x) = (x4 – y4) (x2 + y2 – xy)
= [(x2)2 – (y2)2](x2 + y2 – xy)
= (x2 + y2) (x2 – y2) (x2 + y2 – xy)
(x2 + y2) (x + y) (x – y) (x2 + y2 – xy)
P(x) = x2 + y2 + xy
%20-%20English%20Medium%20Guides.png)









0 Comments:
Post a Comment