12th Physics - Book Back Answers - Unit 1 Electrostatics - English Medium Guides

 

Plus Two / 12th Physics - Book Back Answers - Unit 1 - English Medium

Tamil Nadu Board 12th Standard Physics - Unit 1: Book Back Answers and Solutions

    This post covers the book back answers and solutions for Unit 1 from the Tamil Nadu State Board 12th Standard Physics textbook. These detailed answers have been carefully prepared by our expert teachers at KalviTips.com.

    We have explained each answer in a simple, easy-to-understand format, highlighting important points step by step under the relevant subtopics. Students are advised to read and memorize these subtopics thoroughly. Once you understand the main concepts, you’ll be able to connect other related points with real-life examples and confidently present them in your tests and exams.

    By going through this material, you’ll gain a strong understanding of Unit 1 along with the corresponding book back questions and answers (PDF format).

Question Types Covered:

• 1 Mark Questions: Choose the correct answer, Fill in the blanks, Identify the correct statement, Match the following 
• 2 Mark Questions: Answer briefly 
• 3, 4, and 5 Mark Questions: Answer in detail

All answers are presented in a clear and student-friendly manner, focusing on key points to help you score full marks.

All the best, Class 12 students! Prepare well and aim for top scores. Thank you!

I. Multiple choice questions.

1. Two identical point charges of  magnitude –q are fixed as shown in the figure below. A third charge +q is placed midway between the two charges at the point P. Suppose this charge +q is displaced a small distance from the point P in the directions indicated by the arrows, in which direction(s) will +q be stable with respect to the displacement?

 

(a) A₁ and A₂

(b) B₁ and B₂

(c) both directions

(d) No stable

Answer Key:
(b) B₁ and B₂
 

2. Which charge configuration produces a uniform electric field?
(a) point charge
(b) uniformly charged infinite line
(c) uniformly charged infinite plane
(d) uniformly charged spherical shell
Answer Key:
(c) uniformly charged infinite plane
 

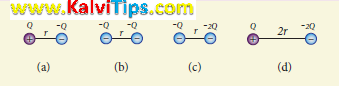
3. What is the ratio of the charges $\left|\frac{{\mathbf{q}}_{\mathbf{1}}}{{\mathbf{q}}_{\mathbf{2}}}\right|$ for the following electric field line pattern?

(a) $\frac{\mathbf{1}}{\mathbf{5}}$

(b) $\frac{\mathbf{22}}{\mathbf{11}}$

(c) 5

(d) $\frac{\mathbf{11}}{\mathbf{25}}$

Answer Key:

(d) $\frac{\mathbf{11}}{\mathbf{25}}$ 

4. An electric dipole is placed at an alignment angle of 30° with an electric field of 2 × 10⁵ NC^-1. It experiences a torque equal to 8 Nm. The charge on the dipole if the dipole length is lcm is
(a) 4 mC
(b) 8 mC
(c) 5 mC
(d) 7 mC
Answer Key:
(b) 8 mC
Hint:
T = PE sin θ
T = (q × 21)E sin30°
q = (q × 10^-2) × $\cancel{2}\times {10}^5\times \frac{1}{\cancel{2}}$ 

q = 8 × 10^-2c

 

5. Four Gaussian surfaces are given below with charges inside each Gaussian surface. Rank the electric flux through each Gaussian surface in increasing order.

(a) D < C < B < A
(b) A < B = C < D
(c) C < A = B < D
(d) D > C > B > A

Answer Key:

(a) D < C < B < A
Hint:
flux depends on charge

 

6. The total electric flux for the following closed surface which is kept inside water.

(a) $\frac{\mathbf{80}\mathbf{q}}{{\mathbf{\in }}_{\mathbf{\circ }}}$

(b) $\frac{\mathbf{q}}{\mathbf{40}{\mathbf{\in }}_{\mathbf{\circ }}}$

(c) $\frac{\mathbf{q}}{\mathbf{80}{\mathbf{\in }}_{\mathbf{\circ }}}$

(d) $\frac{\mathbf{q}}{\mathbf{160}{\mathbf{\in }}_{\mathbf{\circ }}}$

Answer Key: 

(b) $\frac{\mathbf{q}}{\mathbf{40}{\mathbf{\in }}_{\mathbf{\circ }}}$

$\frac{{\mathbf{<b>Hint:</b>}}_{}}{}$

$\frac{{\mathbf{ }}_{}}{}$

7. Two identical conducting balls having positive charges q₁ and q₂ are separated by a center to center distance r. If they are made to touch each other and then separated to the same distance, the force between them will be
(a) less than before
(b) same as before
(c) more than before
(d) zero
Answer Key:
(c) more than before
Hint:

$\mathbf{F}\mathbf{=}\frac{\mathbf{K}\mathbf{\left(}\frac{{\mathbf{q}}_{\mathbf{1}}{\mathbf{q}}_{\mathbf{2}}}{\mathbf{2}}\mathbf{\right)}\mathbf{\left(}\frac{{\mathbf{q}}_{\mathbf{1}}{\mathbf{q}}_{\mathbf{1}}}{\mathbf{2}}\mathbf{\right)}}{{\mathbf{r}}^{\mathbf{2}}}$

$\frac{{\mathbf{F\text{'}>F }}_{}}{}$

$\frac{{\mathbf{ }}_{}}{}$

8. Rank the electrostatic potential energies for the given system of charges in increasing order:

(a) 1 = 4 < 2 < 3
(b) 2 = 4 < 3 < 1
(c) 2 = 3 < 1 < 4
(d) 3 < 1 < 2 < 4
Answer Key:
(a) 1 = 4 < 2 < 3
Hint:

$\frac{{\mathbf{ }}_{}}{}$$\frac{{\mathbf{ }}_{}}{}$

9. An electric field $\overrightarrow{\mathrm{E}}$ = 10 × Î exists in a certain region of space. Then the potential difference V = V_o – V_A, where V_o is the potential at the origin and V_A is the potential at x = 2 m is:
(a) 10 V
(b) -20 V
(c) +20 V
(d) -10 V
Answer Key:
(c) +20 V
Hint:
E = $-\frac{\mathrm{dv}}{\mathrm{dx}}$
dv = E.dx = l0x = 10 × 2
dv = 20 V

 

10. A thin conducting spherical shell of radius R has a charge Q which is uniformly distributed on its surface. The correct plot for electrostatic potential due to this spherical shell is

Answer Key:

Hint:
In a spherical shell, the electric field inside is zero. But the electric potential is constant.
$\mathrm{V}=\frac{\mathrm{q}}{4\mathrm{\pi }{\in }_{\circ }\mathrm{r}}$ as distance increases its potential decrease non-linearly.

 $\frac{{\mathbf{ }}_{}}{}$

11. Two points A and B are maintained at a potential of 7 V and -4 V respectively. The work done in moving 50 electrons from A to B is
(a) 8.80 × 10^-17 J
(b) -8.80 × 10^-17 J
(c) 4.40 × 10^-17 J
(d) 5.80 × 10^-17 J
Answer Key:
(a) 8.80 × 10^-17 J
Hint:
W_A→B = (V_A – V_B)q
=(7+4)ne
= 11 × 50 × 1.6 × 10^-19
=8.8 × 10^-17

 

12. If the voltage applied on a capacitor is increased from V to 2V, choose the correct conclusion.
(a) Q remains the same, C is doubled
(b) Q is doubled, C doubled
(c) C remains the same, Q doubled
(d) Both Q and C remain the same
Answer Key:
(c) C remains the same, Q doubled
Hint:
$\frac{{\mathrm{q}}_2}{{\mathrm{q}}_1}=\frac{\cancel{\mathrm{C}}\left(2\mathrm{V}\right)}{\cancel{\mathrm{C}}\cancel{\mathrm{V}}}$

${\mathrm{Q}}_2=2{\mathrm{Q}}_1$ 

$\frac{{\mathbf{ }}_{}}{}$

13. A parallel plate capacitor stores a charge Q at a voltage V. Suppose the area of the parallel plate capacitor and the distance between the plates are each doubled then which is the quantity that will change?
(a) Capacitance
(b) Charge
(c) Voltage
(d) Energy density
Answer Key:
(d) Energy density

14. Three capacitors are connected in a triangle as shown in the figure. The equivalent capacitance between points A and C is
(a) 1 μF
(b) 2 μF
(c) 3 μF
(d) $\frac{1}{4}$ μF
Answer Key:
(b) 2 μF
Hint:

15. Two metallic spheres of radii 1 cm and 3 cm are given charges of -1 × 10^-2 C and 5 × 10^-2 C respectively. If these are connected by a conducting wire, the final charge on the bigger sphere is
(a) 3 × 10^-2 C
(b) 4 × 10^-2 C
(c) 1 × 10^-2 C
(d) 2 × 10^-2 C
Answer Key:
(a) 3 × 10^-2 C
Hint:
Total charge Q = q₁ + q₂ = 4 × 10^-2 C
charge on bigger sphere,
q₂ = Q($\frac{{\mathrm{r}}_2}{{\mathrm{r}}_1+{\mathrm{r}}_2}$)
= 4 × 10^-2 ×$\frac{3}{4}$
q₂ = 3 × 10^-2 C

II. Short answer questions.

1. What is meant by quantisation of charge?
Answer key:

The charge q on any object is equal to an integral multiple of fundamental unit of charge e. This is called quantisation of electric charge.  Charge of electron  = - 1.6 X 10^-19 C .
q=ne
n is any integer (0 , + 1, + 2, + 3…)
This is called quantisation of charge.

 

2. Write down the Coulomb’s law in vector form and mention what each term  represents. 
Answer Key:   
Coulomb’s law states that, Electrostatic force is directly proportional to the product of the magnitude of the point  charges  and  inversely proportional  to  the  square  of  the  distance  between two point charges.

${\overrightarrow{\mathrm{F}}}_{21}=\frac{{\mathrm{Fq}}_1{\mathrm{q}}_2}{{\mathrm{r}}^2}{\widehat{\mathrm{r}}}_{12}$

F₂₁ = Force on point charge q₂ exerted by another point charge q₁

q₁ q₂ = Point charges                 

r₁₂ = Unit vector

 

3.What are the differences between Coulomb force and gravitational force?

Answer Key: 

S.No	Coulomb Force	Gravitational Force
1	It may be attractive or repulsive.	It is always attractive in nature.
2	It depends upon medium.	It does not depend upon the medium.
3	It is always greater in magnitude. K=9x109 Nm2 C-2	It is lesser than coulomb force. G=6.67x10-11 Nm2 Kg2.

 

4. Write short note on superposition principle. 
Answer Key:
When a number of charges are interacting the total force of a given charge is the vector  sum of the individual forces exerted on the given charge by all the other charges. 
${\overrightarrow{\mathbf{F}}}_{\mathbf{1}}^{\mathbf{t}\mathbf{o}\mathbf{t}}\mathbf{=}{\overrightarrow{\mathbf{F}}}_{\mathbf{12}}\mathbf{+}{\overrightarrow{\mathbf{F}}}_{\mathbf{13}}\mathbf{+}{\overrightarrow{\mathbf{F}}}_{\mathbf{14}}\mathbf{.}\mathbf{.}\mathbf{.}\mathbf{+}{\overrightarrow{\mathbf{F}}}_{\mathbf{1}\mathbf{n}}$

${\overrightarrow{\mathbf{F}}}_{\mathbf{1}}^{\mathbf{t}\mathbf{o}\mathbf{t}}$=F{$\begin{array}{l}\frac{{\mathbf{q}}_{\mathbf{1}}{\mathbf{q}}_{\mathbf{2}}}{{\mathbf{r}}_{\mathbf{21}}^{\mathbf{2}}}\end{array}{\widehat{\mathbf{r}}}_{\mathbf{21}}\mathbf{+}\frac{{\mathbf{q}}_{\mathbf{1}}{\mathbf{q}}_{\mathbf{2}}}{{\mathbf{r}}_{\mathbf{31}}^{\mathbf{2}}}{\widehat{\mathbf{r}}}_{\mathbf{31}}\mathbf{+}\mathbf{.}\mathbf{.}\mathbf{.}\frac{{\mathbf{q}}_{\mathbf{1}}{\mathbf{q}}_{\mathbf{n}}}{{\mathbf{r}}_{\mathbf{n}\mathbf{1}}^{\mathbf{2}}}{\widehat{\mathbf{r}}}_{\mathbf{n}\mathbf{1}}$}

5. Define electric field.

Answer Key:

The electric field at the point P at a distance r from the point charge q is the force  experienced by a unit charge .

$\overrightarrow{\mathbf{E}}\mathbf{=}\frac{\overrightarrow{\mathbf{F}}}{\mathbf{q}\mathbf{0}}\mathbf{=}\frac{\mathbf{k}\mathbf{q}}{{\mathbf{r}}^{\mathbf{2}}}\widehat{\mathbf{r}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{0}}}\frac{\mathbf{q}}{{\mathbf{r}}^{\mathbf{2}}}\widehat{\mathbf{r}}$

SI unit: NC^-1                                                                          

 

6. What is meant by “electric field lines”? 
Answer key:
Electric field vectors are visualized by the concept of electric field lines.
They form a set of continuous lines which represent the electric field in some region of space visually. 

 

7. The electric field lines never intersect . Justify. 
Answer Key:
If some charge is placed in the intersection point , then it has to move in two different directions  at the same time  which is physically impossible. Hence , electric field lines do not intersect. 

 

8. Define electric dipole . Give the expression for the magnitude of its electric dipole moment  and the direction. 
Answer Key:
Electric diapole:
    Two equal and opposite charges separated by a small distance constitute an electric dipole.
$\overrightarrow{\mathbf{P}}\mathbf{=}\mathbf{q}{\overrightarrow{\mathbf{r}}}_{\mathbf{+}}\mathbf{+}\mathbf{(}\mathbf{-}\mathbf{q}\mathbf{)}\overrightarrow{\mathbf{r}}$
Magnitude of the electric dipole:
    Magnitude of the electric dipole moment is equal to the product of the magnitude of one of the charges and the distance between them.
$\left|\overrightarrow{\mathbf{P}}\right|\mathbf{=}\mathbf{2}\mathbf{q}\mathbf{a}$

$\mathbf{ }$

9. Write the general  definition of electric dipole moment for a collection of point charge. 
Answer Key:
The electric dipole moment for a collection of n point charges is given by where ${\overrightarrow{\mathbf{r}}}_{\mathbf{i}}$ is the position vector of charge q_i from the origin.

$\overrightarrow{\mathbf{P}}\mathbf{=}\mathbf{\sum }_{\mathbf{i}\mathbf{=}\mathbf{1}}^{\mathbf{n}}{\mathbf{q}}_{\mathbf{i}}{\overrightarrow{\mathbf{r}}}_{\mathbf{i}}$ 

 

10.  Define "electrostatic potential"?. 
Answer Key:
Electric potential at a point P is equal to the work done force to bring unit positive charge with  constant velocity from infinity to the point P  in the region of the external electric field. 
${\mathbf{V}}_{\mathbf{p}\mathbf{=}\mathbf{-}}\underset{\mathbf{\infty }}{\overset{\mathbf{p}}{\mathbf{\int }}}\overrightarrow{\mathbf{E}}\mathbf{.}\mathbf{d}\overrightarrow{\mathbf{r}}$

$\stackrel{}{\mathbf{ }}$

11.  What is an Equi-potential surface ? 
Answer Key:
An equipotential  surface is a surface  on which all the points are at the same  electric potential. 

12.  What are the properties of an equipotential surface ? 
Answer Key:
1. The work done to move a charge q between any two points A and B, W = q (VB – VA).  
2. If the points  A and B  lie on same equipotential surface Work done is zero because V_A = V_B  
3. The electric field is always normal to an equipotential surface. 

13.  Give the relation between electric field and electric potential.

Answer Key: 

1. Consider a positive charge q kept fixed at the origin. 

2. To move a unit positive charge by a small distance dx towards q in the electric field E, the work done is given by dW = −E dx. 

3. The minus sign implies that work is done against the electric field. 

4. This work done is equal to electric potential difference. Therefore,

dW = dV.

(or) dV = −E dx

Hence $\mathbf{E}\mathbf{=}\mathbf{-}\frac{\mathbf{d}\mathbf{V}}{\mathbf{d}\mathbf{x}}$ 

 

14. Define electrostatic potential energy. 
Answer Key:
Electric potential energy is defined as the work done in bringing the various charges to their  respective positions from infinitely large mutual separation. 

 

15. Define electric flux. 
Answer Key:
The number of electric field lines crossing a given area kept normal to the electric field lines is called electric flux.

${\mathrm{\Phi }}_{\mathrm{E}}=\overrightarrow{\mathrm{E}}.\overrightarrow{\mathrm{A}}=\mathrm{EA}cos\mathrm{\theta }$

16. What is meant by electrostatic energy density?
Answer Key:
The energy stored per unit volume of space is defined electrostatic energy density.
${\mathrm{U}}_{\mathrm{E}}=\frac{\mathrm{U}}{\mathrm{Volume}}=\frac{1}{2}{\in }_{\circ }{\mathrm{E}}^2$
U – electrostatic potential energy
E – electric field
${\in }_{\circ }$ – permittivity of free space

 

17. Write a short note on electrostatic shielding. 
Answer Key:
The phenomenon of protecting a region of space from any external electric field is called as electrostatic shielding .
Consider a cavity inside the conductor whatever the charges at the surfaces and whatever the electrical disturbances outside, the electric field inside cavity is zero.      
Ex: Faraday Cage 

18. What is Polarisation?
Answer Key:
Polarisation is defined as the total dipole moment per unit volume of the dielectric.

$\overrightarrow{\mathrm{p}}={\mathrm{\chi }}_{\mathrm{e}}{\overrightarrow{\mathrm{E}}}_{\mathrm{ext}}$
χe= electric susceptibility 

 

19.What is dielectric strength ?

Answer Key:

The maximum electric field the dielectric can withstand before it breakdown is called dielectric strength.

For example: Dielectric strength of air 3 X 10⁶ V m^-1

 

20. Define capacitance. Give its unit.
Answer Key:
The capacitance C of a capacitor is defined as the ratio of the magnitude of charge on either of the conductor plates to the potential difference existing between them.  

$\mathbf{C}\mathbf{=}\frac{\mathbf{Q}}{\mathbf{V}}$ 

 

21. What is corona discharge ? 
Answer Key:
1. The  total charge of the charged conductor near the sharp edge reduces. 
2. Leakage of charges from the sharp points to the charged conductor.
3. Corona discharge also known as "action of points"

III. Long answer questions. 

1. Discuss the basic properties of electric charges.

Answer Key:
1. Electric Charge :

• Objects in the universe are made up of atoms which made up of protons , neutrons, and electrons.
• These particles have mass , an inherent property of particles.
• Electric charge is another intrinsic and fundamental property of particles. 
• The  SI  unit of  charge  is   Coulomb.

2. Conservation of Charge :

• The  total electric charge in the universe is constant. Charge can neither be created nor be destroyed.  
• In any  physical process  net change in charge will always be zero.
• Objects are electrically neutral before rubbing process happen.
• After rubbing simply transfers charges from one object to the others.

Example :
   1. When a glass rod rubbed with silk cloth then negative charge transferred from glass to silk.
   2. As a result , glass rod is positively charged and silk cloth is negatively charged.

 

3. Quantisation of Charge: 

• The charge q on any object is equal to an integral multiple of fundamental unit of charge e. This is called quantisation of electric charge.  Charge of electron  = - 1.6 X 10^-19 C .
• q=ne
• n is any integer (0 , + 1, + 2, + 3…)
• This is called quantisation of charge.

2. Explain in detail Coulomb’s law and its various aspects.
Answer Key:

1. Coulomb’s law states that, Electrostatic force is directly proportional to the product of the magnitude of the point  charges  and  inversely proportional  to  the  square  of  the  distance  between two point charges.

${\overrightarrow{\mathrm{F}}}_{21}=\frac{{\mathrm{Fq}}_1{\mathrm{q}}_2}{{\mathrm{r}}^2}{\widehat{\mathrm{r}}}_{12}$

F₂₁ = Force on point charge q₂ exerted by another point charge q₁

q₁ q₂ = Point charges                 

r₁₂ = Unit vector

 

2. The force on the charge q2 exerted by the charge q1 always lies along the line joining the two charges. $\frac{{\mathrm{}}^{}}{}{\widehat{\mathrm{r}}}_{12}$ is the unit vector pointing from charge q1 to q2 . 

 

3. In SI units,  and its value is 9 X 10⁹  N m² C^-2. Here ε₀ is the permittivity of free space or vacuum and its value is ${\mathbf{\in }}_{\mathbf{\circ }}\mathbf{=}\frac{\mathbf{1}}{\mathbf{4}\mathbf{\pi }\mathbf{k}}\mathbf{=}\mathbf{8.85}\mathbf{\times }{\mathbf{10}}^{\mathbf{-}\mathbf{12}}{\mathbf{C}}^{\mathbf{2}}{\mathbf{N}}^{\mathbf{-}\mathbf{1}}{\mathbf{m}}^{\mathbf{-}\mathbf{2}}$

 

4. The magnitude of the electrostatic force between two charges each of one coulomb and separated by a distance of 1 m is calculated as follows:$\left|\mathbf{ F}\right|\mathbf{=}\frac{\mathbf{9}\mathbf{\times }{\mathbf{10}}^{\mathbf{9}}\mathbf{\times }\mathbf{1}\mathbf{\times }\mathbf{1}}{{\mathbf{1}}^{\mathbf{2}}}\mathbf{=}\mathbf{9}\mathbf{\times }{\mathbf{10}}^{\mathbf{9}}\mathbf{N}$

 

5. In SI units, Coulomb’s law in vacuum

${\overrightarrow{\mathbf{F}}}_{\mathbf{12}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{\circ }}}\frac{{\mathbf{q}}_{\mathbf{1}}{\mathbf{q}}_{\mathbf{2}}}{{\mathbf{r}}^{\mathbf{2}}}{\widehat{\mathbf{r}}}_{\mathbf{12}}$

In a medium

${\overrightarrow{\mathbf{F}}}_{\mathbf{12}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{4}\mathbf{\pi }\mathbf{\in }}\frac{{\mathbf{q}}_{\mathbf{1}}{\mathbf{q}}_{\mathbf{2}}}{{\mathbf{r}}^{\mathbf{2}}}{\widehat{\mathbf{r}}}_{\mathbf{12}}$

 

6. Difference between Coulomb force and gravitational force

S.No	Coulomb Force	Gravitational Force
1	It may be attractive or repulsive.	It is always attractive in nature.
2	It depends upon medium.	It does not depend upon the medium.
3	It is always greater in magnitude. K=9x109 Nm2 C-2	It is lesser than coulomb force. G=6.67x10-11 Nm2 Kg2.

 

7. The force on a charge q₁ exerted by a point charge q₂ is given by 

${\overrightarrow{\mathbf{F}}}_{\mathbf{12}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{\circ }}}\frac{{\mathbf{q}}_{\mathbf{1}}{\mathbf{q}}_{\mathbf{2}}}{{\mathbf{r}}^{\mathbf{2}}}{\widehat{\mathbf{r}}}_{\mathbf{21}}$

Here $\frac{{\mathbf{}}^{}}{}{\widehat{\mathbf{r}}}_{\mathbf{12}}$ is the unit vector from charge q₁ to q₂.

But ${\widehat{\mathbf{r}}}_{\mathbf{21}}\mathbf{=}\mathbf{-}{\widehat{\mathbf{r}}}_{\mathbf{12}}$ 

${\overrightarrow{\mathbf{F}}}_{\mathbf{12}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{\circ }}}\frac{{\mathbf{q}}_{\mathbf{1}}{\mathbf{q}}_{\mathbf{2}}}{{\mathbf{r}}^{\mathbf{2}}}\left(\mathbf{-}{\widehat{\mathbf{r}}}_{\mathbf{12}}\right)\mathbf{=}\mathbf{-}\frac{\mathbf{1}}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{\circ }}}\frac{{\mathbf{q}}_{\mathbf{1}}{\mathbf{q}}_{\mathbf{2}}}{{\mathbf{r}}^{\mathbf{2}}}\left({\widehat{\mathbf{r}}}_{\mathbf{12}}\right)$

(or)${\overrightarrow{\mathbf{F}}}_{\mathbf{12}}\mathbf{=}\mathbf{-}{\overrightarrow{\mathbf{F}}}_{\mathbf{21}}$ 

 

3. Define electric field and discuss its various aspects .
Answer Key:

Electric Field : 
Electric field at a point P, at a distance r from the point charge q is the force  experienced by a unit point charge.     

Formula:
$\overrightarrow{\mathrm{E}}=\frac{\overrightarrow{\mathrm{F}}}{{\mathrm{q}}_0}=\frac{\mathrm{kq}}{{\mathrm{r}}^2}\widehat{\mathrm{r}}=\frac{1}{4\mathrm{\pi }{\in }_0}\frac{\mathrm{q}}{{\mathrm{r}}^2}\widehat{\mathrm{r}}$

SI unit : N C^-1                 

Important aspects of Electric field:
1. Force experienced by the test charge q0 is $\overrightarrow{F}=q_0\overrightarrow{E}$
2. q is positive , electric field points away from the source . 
3. q is negative , electric field points   towards the source . 
4. Electric field is independent of test charge q0 and depends only on source charge q.
5. Electric field is a vector quantity which has unique direction and magnitude . 
6. As  distance increases  electric  field decreases in magnitude.
7. Test charge q0  is small , not modify the electric field of source charge.
8. Electric field equation is only valid for point charges.
9. There  are  two kinds  of the  electric field. Uniform  and non -  uniform  electric field.
10. Uniform  electric field :  Have same direction and constant magnitude  at all points.
11. Non-uniform  electric field : Different directions and different magnitudes or both at different points  in  space. 

 

4. Calculate the electric field due to a dipole on its axial line and equatorial plane.
Answer Key:

Diagram:

Formula:
${\overrightarrow{\mathit{E}}}_{\mathbf{a}\mathbf{x}\mathbf{i}\mathbf{a}\mathbf{l}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{0}}}\frac{\mathbf{2}\overrightarrow{\mathbf{p}}}{{\mathbf{r}}^{\mathbf{3}}}$

Explanation:
Consider an electric dipole placed on the x-axis . A point C is located at a distance of r from the midpoint O of the  dipole on the axial line. Electric dipole moment vector $\frac{\overrightarrow{\mathbf{p}}}{}$ is from -q to +q and is directed along BC.

i) Electric field due to a electric dipole on its axial line:

1. Electric field due to +q: 

2. Electric field due to -q: 

3. Total Electric field:

4. (r >> a)  then  (r²-a²)² = r⁴ 

ii) Electric field due to a electric dipole on its Equatorial plane :
1. Let  a point C at a distance r from the midpoint O  of the dipole on equatorial plane . 
2. The  point  C is  equi distant from +q and – q , magnitude of the electric fields is same.
3. ${\overrightarrow{\mathbf{E}}}_{\mathbf{+}}$ and ${\overrightarrow{\mathbf{E}}}_{\mathbf{-}}$ can be resolved into two components.
4. One  component  parallel to dipole axis  and other  perpendicular to it.
5. Perpendicular components |${\overrightarrow{\mathbf{E}}}_{\mathbf{+}}$| sinθ and |${\overrightarrow{\mathbf{E}}}_{\mathbf{-}}$| sinθ equal in magnitude oppositely directed , they cancel each other. 
6. Magnitude of total electric field is sum of the parallel component of ${\overrightarrow{\mathbf{E}}}_{\mathbf{+}}$,${\overrightarrow{\mathbf{E}}}_{\mathbf{-}}$ direction along $\widehat{\mathbf{p}}$
Diagram:

Formula:
$$E→tot=-14π∈0p→r3

At very large distance (r>>a) then (r² + a²)^3/2 = r³ 

${\overrightarrow{\mathbf{E}}}_{\mathbf{t}\mathbf{o}\mathbf{t}}\mathbf{=}\mathbf{-}\frac{\mathbf{1}}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{0}}}\frac{\overrightarrow{\mathbf{p}}}{{\mathbf{r}}^{\mathbf{3}}}$ 

 

5. Derive an expression for the torque experienced by a dipole due to a uniform electric field.
Answer Key:

Diagram:      

                                                                       

 

Formula:

$\overrightarrow{\mathbf{\tau }}\mathbf{=}$$\frac{\overrightarrow{\mathbf{p}}}{}$x${\overrightarrow{\mathbf{E}}}_{}$=PE$\mathbf{sin}$θ
 

Torque on dipole due to uniform electric field:
1. Consider an electric dipole moment $\frac{\overrightarrow{\mathbf{p}}}{}$ placed in a uniform electric field ${\overrightarrow{\mathbf{E}}}_{}$.
2. Charge +q experience a force:q${\overrightarrow{\mathbf{E}}}_{}$        
3. Charge -q experience a force:-q${\overrightarrow{\mathbf{E}}}_{}$   
4. Total force acts on the dipole is zero. But two forces constitute a couple.
5.The dipole experience a torque tends to rotate the dipole.

Derivation:
1. $\overrightarrow{\mathbf{\tau }}\mathbf{=}\overrightarrow{\mathbf{O}\mathbf{A}}\mathbf{\times (-q}$${\overrightarrow{\mathbf{E}}}_{}$$\mathbf{)}\mathbf{+}\overrightarrow{\mathbf{O}\mathbf{B}}\mathbf{\times }\mathbf{q}\overrightarrow{\mathbf{E}}$ 

2. $\overrightarrow{\mathbf{\tau }}\mathbf{=}$|$\overrightarrow{\mathbf{O}\mathbf{A}}$||($\mathbf{-q}$${\overrightarrow{\mathbf{E}}}_{}$)|sinθ+|$\mathbf{}\overrightarrow{\mathbf{O}\mathbf{B}}$||$\mathbf{q}$${\overrightarrow{\mathbf{E}}}_{}$|sinθ   

3. $\overrightarrow{\mathbf{\tau }}\mathbf{=qE.2asin}$θ

4. $\overrightarrow{\mathbf{\tau }}\mathbf{=}$$\frac{\stackrel{\mathbf{\to ✕}}{\mathbf{p}}}{}$${\overrightarrow{\mathbf{E}}}_{}$    

 

Cases:
1.Magnitude of torque is τ=pE sin θ and is maximum when θ=90°.
2.If $\frac{\overrightarrow{\mathbf{p}}}{}$ is aligned with ${\overrightarrow{\mathbf{E}}}_{}$, the total torque on the dipole becomes zero. 

 

6. Derive an expression for electrostatic potential due to a point charge.
Answer Key:

Diagram:

Formula:
$V=\frac{1}{4\pi {\in }_0}\frac{q}{r}$
 

Explanation:     
Consider a positive charge q kept fixed at a origin . Let P be a point at distance r from charge q.

Derivation:
1. Electric potential at the point P: $\mathbf{ }$

$\mathbf{V}\mathbf{=}\underset{\mathbf{\infty }}{\overset{\mathbf{r}}{\mathbf{\int }}}$(-$\overrightarrow{\mathbf{E}}$)$\mathbf{.}\mathbf{d}\overrightarrow{\mathbf{r}}\mathbf{=}\mathbf{-}\underset{\mathbf{\infty }}{\overset{\mathbf{r}}{\mathbf{\int }}}\overrightarrow{\mathbf{E}}\mathbf{.}\mathbf{d}\mathbf{r}$

2. Electric field due to positive point charge q:$$$\overrightarrow{\mathbf{E}}$$\mathbf{=}\frac{\mathbf{1}}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{0}}}\frac{\mathbf{q}}{{\mathbf{r}}^{\mathbf{2}}}\widehat{\mathbf{r}}$
3. $\mathbf{V}\mathbf{=}\frac{\mathbf{-}\mathbf{1}}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{0}}}\underset{\mathbf{\infty }}{\overset{\mathbf{r}}{\mathbf{\int }}}\frac{\mathbf{q}}{{\mathbf{r}}^{\mathbf{2}}}\widehat{\mathbf{r}\mathbf{.}}\mathbf{d}\overrightarrow{\mathbf{r}}$
4. The infinitesimal displacement vector $\overrightarrow{\mathbf{d}\mathbf{r}}\mathbf{=}\mathbf{d}\mathbf{r}\widehat{\mathbf{r}}$ and using $\widehat{\mathrm{r}}.\widehat{\mathrm{r}}=1$
5. $\mathrm{V}=-\frac{1}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{0}}}\underset{\mathbf{\infty }}{\overset{\mathbf{r}}{\mathbf{\int }}}\frac{\mathbf{q}}{{\mathbf{r}}^{\mathbf{2}}}\widehat{\mathbf{r}\mathbf{.}}\mathbf{d}\mathbf{r}\widehat{\mathbf{r}}\mathbf{=}-\frac{1}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{0}}}\underset{\mathbf{\infty }}{\overset{\mathbf{r}}{\mathbf{\int }}}\frac{\mathbf{q}}{{\mathbf{r}}^{\mathbf{2}}}\mathbf{d}\mathbf{r}$
6. $\mathbf{V}\mathbf{=}-\frac{1}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{0}}}q${$-\frac{1}{r}$}^r_¥ $=\frac{\mathbf{1}}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{0}}}\frac{q}{r}$

 

Cases:

Charge q	Potential	V Value	Distance
Positive	V=$\frac{1}{4\pi {\in }_0}\frac{q}{r}$	Decreases	Increases
Neagative	V=$\frac{1}{4\pi {\in }_0}\frac{q}{r}$	Increases	Increases

 

7. Derive an expression for electrostatic potential due to an electric dipole.
Answer Key:

Diagram: 

 

Formula:
$\mathbf{V}\mathbf{=}\frac{1}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{\circ }}}\frac{\overrightarrow{p}.\widehat{r}}{r^2}$
 

Explanation 
Consider two equal and opposite charges separated by a small distance 2a.
The point P is located at a distance r from the midpoint of the dipole.
Let θ be  the  angle  between  the line  OP  and  dipole  axis AB.
Let r1 be the distance of point P from +q. Let r2 be the distance of point P from -q. 

 

Derivation:
1. Potential at P due to charge +q: $\mathbf{=}\frac{1}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{\circ }}}\frac{q}{r_1}$
2. Potential at P due to charge -q: $=-\frac{1}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{\circ }}}\frac{q}{r_2}$
3. Total Potential: $\mathrm{V}=\frac{1}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{\circ }}}q$($\frac{\mathbf{1}}{{\mathbf{r}}_{\mathbf{1}}}\mathbf{-}\frac{\mathbf{1}}{{\mathbf{r}}_{\mathbf{2}}}$)

 

Special cases:

 

8. Obtain expression for potential energy due to collection of three point charges which are separated by finite distance.    
Diagram:

Formula:

$\mathbf{U}\mathbf{=}\frac{\mathbf{1}}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{\circ }}}$ 

 

Explanation :

1.  Bringing a charge q₁ from infinity to the point A requires no work _. 

2. To bring the second charge q₂ to the point B , work must be done against the electric field created by the charge q₁ .

 The work done on the charge q₂ is  W =  ₂V_1B . V_1B  is the electrostatic potential due to charge q₁ at point B.

${\mathbf{U}}_{\mathbf{I}\mathbf{ }}\mathbf{=}\frac{\mathbf{1}}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{\circ }}}\frac{{\mathbf{q}}_{\mathbf{1}}{\mathbf{q}}_{\mathbf{2}}}{{\mathbf{r}}_{\mathbf{12}}}$ 

3. To bring the charge q₃ to the point C, work must be done against  total electric  field due to both   charges q₁  and q₂.         

1. The work done to bring the charge q₃  is W = q₃ ( V_1C + V_2C) 

2. V_1C is the electrostatic  potential due to charge q₁ at point C.

3. V_2C is the electrostatic potential due to charge q₂ at point C.

${\mathbf{U}}_{\mathbf{I}\mathbf{I}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{4}\mathbf{\pi }{\mathbf{\in }}_{\mathbf{\circ }}}$

4. Total electrostatic potential energy for the system of charges.

$U_{III}=\frac{1}{4\pi {\in }_{\circ }}$

5. Electrostatic potential is independent of configuration of charges since force is  conservative one.

 

9. Derive an expression for electrostatic potential energy of the dipole in a uniform electric field.
Diagram:

Formula:

U=-pEcosθ=-$\frac{\stackrel{\mathbf{\to .}}{\mathbf{p}}}{}$${\overrightarrow{\mathbf{E}}}_{}$
 

Explanation: 

1. Consider a dipole placed in the uniform electric field ${\overrightarrow{\mathbf{E}}}_{}$.

2. A dipole experiences a torque when kept in an uniform electric field ${\overrightarrow{\mathbf{E}}}_{}$.

3. This torque rotates the dipole to align it with the direction of the electric field.

4. Rotate the dipole from its initial angle θ to another angle θ′against the torque.

5. An equal and opposite external torque must be applied on the dipole.

 

Derivation:

1. Work done by the external torque $\mathbf{W}\mathbf{=}\underset{\mathbf{\theta }\mathbf{\text{'}}}{\overset{\mathbf{\theta }}{\mathbf{\int }}}{\mathbf{\tau }}_{\mathbf{e}\mathbf{x}\mathbf{t}}\mathbf{d}\mathbf{\theta \; \to (1)}$

2. |${\overrightarrow{\mathbf{\tau }}}_{\mathbf{e}\mathbf{x}\mathbf{t}}$|=|${\overrightarrow{\mathbf{\tau }}}_{\mathbf{E}}$|=|$\frac{\overrightarrow{\mathbf{p}}}{}$x${\overrightarrow{\mathbf{E}}}_{}$| $\mathbf{\to \; (2) }$

3. Substituting equation (2) in equation (1), we get 

$\mathbf{W}\mathbf{=}\underset{\mathbf{\theta }\mathbf{\text{'}}}{\overset{\mathbf{\theta }}{\mathbf{\int }}}\mathbf{p}\mathbf{E}\mathbf{s}\mathbf{i}\mathbf{n}\mathbf{\theta }\mathbf{d}\mathbf{\theta }$  

4.  This work done is equal to the potential energy difference.

U(θ)-U(θ′)=∆U=-pEcosθ+pEcosθ′

5. Initial angle is θ′= 90° as reference point ,  then U (θ′)=pEcos90^°=0   

6. Potential energy: U(θ) = - pEcosθ = -$\frac{\stackrel{\mathbf{\to .}}{\mathbf{p}}}{}$${\overrightarrow{\mathbf{E}}}_{}$  

 

Cases :

1. Potential energy is maximum when dipole is aligned anti – parallel ( θ = π )  to  electric field.

2. Potential energy is minimum when dipole is aligned parallel ( θ = 0 )  to the external electric field.

 

10. Obtain Gauss law from Coulomb’s law.       

    Gauss’s law states that if a charge Q is enclosed by an arbitrary closed surface, then the total electric flux Φ_E through the closed surface is ${\mathbf{\Phi }}_{\mathbf{E}}\mathbf{\oint }\overrightarrow{\mathbf{E}}\mathbf{.}\mathbf{d}\overrightarrow{\mathbf{A}}\mathbf{=}\frac{{\mathbf{Q}}_{\mathbf{e}\mathbf{n}\mathbf{c}\mathbf{l}}}{{\mathbf{\in }}_{\mathbf{\circ }}}$

$\frac{{\mathbf{<b>Diagram:</b>}}_{}}{}$

$\frac{{\mathbf{<b> </b>}}_{}}{}$

$\frac{{\mathbf{<b>Formula:</b>}}_{}}{}$

${\mathbf{\Phi }}_{\mathbf{E}}\mathbf{\oint }\overrightarrow{\mathbf{E}}\mathbf{.}\mathbf{d}\overrightarrow{\mathbf{A}}\mathbf{=}\frac{{\mathbf{Q}}_{\mathbf{e}\mathbf{n}\mathbf{c}\mathbf{l}}}{{\mathbf{\in }}_{\mathbf{\circ }}}$$\frac{{\mathbf{ }}_{}}{}$

$\frac{{\mathbf{<b> </b>}}_{}}{}$

$\frac{{\mathbf{<b>Derivation:</b>}}_{}}{}$

$\frac{{\mathbf{1.\; A\; positive\; point\; charge\; Q\; is\; surrounded\; by\; an\; imaginary\; sphere\; of\; radius\; r.}}_{}}{}$

$\frac{{\mathbf{2.The\; total\; electric\; flux\; through\; the\; closed\; surface\; of\; the\; sphere\; using }}_{}}{}$

$\frac{{\mathbf{3.\; d}}_{}}{}$$\mathbf{}\overrightarrow{\mathbf{A}}$$\frac{{\mathbf{ is\; along\; the\; electric\; field }}_{}}{}$${\stackrel{\mathbf{\to }}{\mathbf{E}}}_{}$$\frac{{\mathbf{<math\; xmlns="http://www.w3.org/1998/Math/MathML"><mi\; mathvariant="normal">\theta </mi></math>}}_{}}{}$$\frac{{\mathbf{=0°. }}_{}}{}$

$\frac{{\mathbf{4.\; E\; is\; uniform\; on\; the\; surface\; of\; the\; sphere, }}_{}}{}$

4πr²

$\frac{{\mathbf{<math\; xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi\; mathvariant="bold">\Phi </mi><mi\; mathvariant="bold">E</mi></msub></math>}}_{}}{}$

11. Obtain the expression for electric field due to an infinitely long charged wire.

Diagram:

Formula:

$\overrightarrow{E}=\frac{1}{2\pi {\in }_{\circ }}\frac{\lambda }{r}\widehat{r}$ 

 

Theory :                                                                                                                                                                 

1. Consider an infinitely long straight wire having uniform linear charge density λ .

2. Let P be a point located at a perpendicular distance r from the wire. The electric field  can be found using Gauss law.

3. Two small charge elements A₁ ,A₂ on the wire which are at equal distances  from  point P.

4. Resultant electric field due to two charge elements points radially away from charged wire.

5. The magnitude of electric field is same at all points on the circle of radius r.

6. The charged wire possesses a cylindrical symmetry, Gaussian  surface of radius r  and length L.  

 

Derivation:

1. Total electric flux through the closed surface ${\mathit{\Phi }}_{\mathit{E}}\mathbf{=}\mathbf{\oint }\overrightarrow{\mathit{E}\mathbf{.}}\mathit{d}\overrightarrow{\mathit{A}}$  

2.  $\underset{\mathbf{C}\mathbf{u}\mathbf{r}\mathbf{v}\mathbf{e}\mathbf{d}\mathbf{ }\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{f}\mathbf{a}\mathbf{c}\mathbf{e}}{\mathbf{\int }\mathbf{ }}\overrightarrow{\mathit{ E}\mathbf{.}}\mathit{d}\overrightarrow{\mathit{A}}\mathbf{+}\underset{\mathbf{t}\mathbf{o}\mathbf{p}\mathbf{ }\mathbf{surface}}{\mathbf{\int }\mathbf{ }}\overrightarrow{\mathit{E}\mathbf{.}}\mathit{d}\overrightarrow{\mathit{A}}\mathbf{+}\underset{\mathit{b}\mathit{o}\mathit{t}\mathit{t}\mathit{o}\mathit{m}\mathbf{ }\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{f}\mathbf{a}\mathbf{c}\mathbf{e}}{\mathbf{\int }\mathbf{ }}\overrightarrow{\mathit{E}\mathbf{.}}\mathit{d}\overrightarrow{\mathit{A}}$      

3.  For  the curved surface:  E is   parallel   to  A  then  ,   E  . d A   =   E  d A

4. For the  top and bottom surface :   E  is perpendicular to  A  then ,  E  .  d A   =   0 . 

5. Applying Gauss law to the cylindrical surface ,   ${\mathit{\Phi }}_{\mathit{E}}\mathbf{=}\underset{\mathbf{C}\mathbf{u}\mathbf{r}\mathbf{v}\mathbf{e}\mathbf{d}\mathbf{ }\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{f}\mathbf{a}\mathbf{c}\mathbf{e}}{\mathbf{\int }\mathbf{ }}\mathit{E}\mathit{d}\mathit{A}\mathbf{=}\frac{{\mathit{Q}}_{\mathit{e}\mathit{n}\mathit{c}\mathit{l}}}{{\mathit{ϵ}}_{\mathit{o}}}$

6. The  magnitude  of  the  electric  field  for  the  entire  curved  surface  is  constant.                                 7.  Linear  charge  density  (charge per unit length) : $$\begin{gathered} {\mathit{\Phi }}_{\mathit{E}}\mathbf{=}\mathbf{\oint }\overrightarrow{\mathit{E}\mathbf{.}}\mathit{d}\overrightarrow{\mathit{A}}\text{ \\ ∫ Curved surfaceE.→dA→+∫ top surfaceE.→dA→+∫ bottom surfaceE.→dA→ \\ ΦE=∫ Curved surfaceEdA=Qenclϵο \\ E ∫ Curved surfacedA=λLϵο \\ ∫ Curved surfacedA=2πrL \\ E.2πrL =λLϵο \\ E=12πϵολr \\ E→=12πϵο λr r^ \\ Qencl=λL} \end{gathered}$$

8. $\mathit{E} \underset{\mathbf{C}\mathbf{u}\mathbf{r}\mathbf{v}\mathbf{e}\mathbf{d}\mathbf{ }\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{f}\mathbf{a}\mathbf{c}\mathbf{e}}{\mathbf{\int }\mathbf{ }}\mathit{d }\mathit{A}\mathbf{=}\frac{\mathit{\lambda }\mathit{L}}{{\mathit{ϵ}}_{\mathit{o}}}$      

9. Total area of the curved surface : $\underset{\mathbf{C}\mathbf{u}\mathbf{r}\mathbf{v}\mathbf{e}\mathbf{d}\mathbf{ }\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{f}\mathbf{a}\mathbf{c}\mathbf{e}}{\mathbf{\int }\mathbf{ }}\mathit{d }\mathit{A}\mathbf{=}\mathbf{2}\mathit{\pi }\mathit{r}\mathit{L}$

10. $\mathit{E}\mathbf{.}\mathbf{2}\mathit{\pi }\mathit{r}\mathit{L}\mathbf{ }\mathbf{=}\frac{\mathit{\lambda }\mathit{L}}{{\mathit{ϵ}}_{\mathit{o}}}$

11. Electric field due to infinite long charged wire: $\mathit{E}\mathbf{=}\frac{\mathbf{1}}{\mathbf{2}\mathit{\pi }{\mathit{ϵ}}_{\mathit{o}}}\frac{\mathit{\lambda }}{\mathit{r}}$

12. In vector form: $\overrightarrow{\mathit{E}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{2}\mathit{\pi }{\mathit{ϵ}}_{\mathit{o}}} \frac{\lambda }{r} \widehat{r}$

13. If   λ  >  0  then   E   points perpendicularly  outward  (  r  )  from the wire.

14. If   λ < 0  then   E   points perpendicularly  inward  ( - r  )  from the wire

 

12. Obtain the expression for electric field due to a charged infinite plane sheet.

 Diagram:    

Formula:
$\overrightarrow{\mathbf{E}}\mathbf{=}\frac{\mathbf{\sigma }}{\mathbf{2}\mathbf{ }{\mathbf{ϵ}}_{\mathbf{o}}}\widehat{\mathbf{n}}$                                                                              

Explanation:

1.An infinite plane sheet of charges with uniform surface charge density  σ 

2. Let P be a point at a distance r from the sheet.

3. The  electric field should be same at all points equidistant from  the plane.

4. A cylindrical Gaussian surface of length 2r and two flats surface each of area A is chosen.

5. The infinite plane sheet passes perpendicularly through the middle part of the Gaussian surface.

 

 Derivation:

1.  Total electric flux linked with the cylindrical surface  ${\mathit{\Phi }}_{\mathit{E}\mathbf{=}}\mathbf{\oint }\overrightarrow{\mathit{E}}\mathbf{.}\mathit{d}\overrightarrow{\mathit{A}}$  

2. ${\mathit{\Phi }}_{\mathit{E}\mathbf{=}}\mathbf{=}\underset{\mathit{C}\mathit{u}\mathit{r}\mathit{v}\mathit{e}\mathit{d}\mathbf{ }\mathit{s}\mathit{u}\mathit{r}\mathit{f}\mathit{a}\mathit{c}\mathit{e}}{\mathbf{\int }}\overrightarrow{\mathit{E}}\mathbf{.}\mathit{d}\overrightarrow{\mathit{A}}\mathbf{+}\underset{\mathit{P}}{\mathbf{\int }}\overrightarrow{\mathit{E}}\mathbf{.}\mathit{d}\overrightarrow{\mathit{A}}\mathbf{+}\underset{\mathit{P}\mathbf{\text{'}}}{\mathbf{\int }}\overrightarrow{\mathit{E}}\mathbf{.}\mathit{d}\overrightarrow{\mathit{A}}\mathbf{=}\frac{{\mathit{Q}}_{\mathit{e}\mathit{n}\mathit{c}\mathit{l}}}{{\mathbf{ϵ}}_{\mathbf{o}}}$

3. For curved surface :  Electric field is perpendicular to the area  ${\mathit{\Phi }}_{\mathit{E}\mathbf{=}}\mathbf{=}\underset{\mathit{C}\mathit{u}\mathit{r}\mathit{v}\mathit{e}\mathit{d}\mathbf{ }\mathit{s}\mathit{u}\mathit{r}\mathit{f}\mathit{a}\mathit{c}\mathit{e}}{\mathbf{\int }}\overrightarrow{\mathit{E}}\mathbf{.}\mathit{d}\overrightarrow{\mathit{A}}\mathbf{+}\underset{\mathit{P}}{\mathbf{\int }}\overrightarrow{\mathit{E}}\mathbf{.}\mathit{d}\overrightarrow{\mathit{A}}\mathbf{+}\underset{\mathit{P}\mathbf{\text{'}}}{\mathbf{\int }}\overrightarrow{\mathit{E}}\mathbf{.}\mathit{d}\overrightarrow{\mathit{A}}\mathbf{=}\frac{{\mathit{Q}}_{\mathit{e}\mathit{n}\mathit{c}\mathit{l}}}{{\mathbf{ϵ}}_{\mathbf{o}}}$                          

4.  At  P  and  P :  Electric field is   parallel to the area element at all points.                                                  5.  By  applying  Gauss law , ${\mathit{\Phi }}_{\mathit{E}\mathbf{=}}\underset{\mathit{P}}{\mathbf{\int }}\mathit{E}\mathit{d}\mathit{A}\mathbf{+}\underset{\mathit{P}\mathbf{\text{'}}}{\mathbf{\int }}\mathit{E}\mathit{d}\mathit{A}\mathbf{=}\frac{{\mathit{Q}}_{\mathit{e}\mathit{n}\mathit{c}\mathit{l}}}{{\mathbf{ϵ}}_{\mathbf{o}}}$

6. Magnitude  of  the electric field  at  these  two  equal  flat  surfaces is uniform ,  E  is  taken out of the  integration .                                                      

7. ${\mathit{Q}}_{\mathit{e}\mathit{n}\mathit{c}\mathit{l}}\mathbf{=}\mathbf{\sigma }\mathbf{A}$

8. $\mathbf{2}\mathbf{E}\mathbf{ }\underset{\mathit{P}}{\mathbf{\int }}\mathit{d}\mathit{A}\mathbf{=}\frac{\mathbf{\sigma }\mathbf{A}}{{\mathbf{ϵ}}_{\mathbf{o}}}$

9.  The   total  area   of  surface  either  at  P  and $\underset{\mathit{P}}{\mathbf{\int }}\mathit{d}\mathit{A}\mathbf{=}\mathit{A}$

10. $\mathbf{2}\mathit{E}\mathit{A}\mathbf{=}\frac{\mathbf{\sigma }\mathbf{A}}{{\mathbf{ϵ}}_{\mathbf{o}}}$

11. $\overrightarrow{E}=\frac{\mathbf{\sigma }}{\mathbf{2}\mathbf{ }{\mathbf{ϵ}}_{\mathbf{o}}}$

12. In  vector  form $\overrightarrow{\mathbf{E}}\mathbf{=}\frac{\mathbf{\sigma }}{\mathbf{2}\mathbf{ }{\mathbf{ϵ}}_{\mathbf{o}}}\widehat{\mathbf{n}}$

13. If  σ  >  0  then   E   points perpendicularly  outward   to the plane   (n).

14. If  σ < 0  then   E   points perpendicularly  inward to the plane  (-n).

 

13. Obtain the expression for electric field due to a uniformly charged spherical shell.

1.  Consider a uniformly charged spherical shell of radius R  and total charge  Q  .

2. The electric field at points outside and inside the sphere can be found using Gauss law.

 Case  i :   At a point outside the shell (  r   >   R )

For point outside the spherical shell , a large spherical Gaussian surface is drawn .

1. Let us choose a point P  outside the shell at a distance  r from the centre.

2. The charge is uniformly distributed on the surface of the sphere. ( spherically symmetry )

3. The electric field must point radially outward if  Q  >  0.   4. The electric field must point radially inward if  Q  <  0.

 

Derivation:

 1. Applying Gauss law: $\underset{\mathbf{G}\mathbf{a}\mathbf{u}\mathbf{s}\mathbf{s}\mathbf{i}\mathbf{a}\mathbf{n}\mathbf{ }\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{f}\mathbf{a}\mathbf{c}\mathbf{e}}{\mathbf{\oint }}\overrightarrow{\mathbf{E}}\mathbf{.}\mathbf{d}\overrightarrow{\mathbf{A}}$

 2. $\mathbf{E}\mathbf{ }\underset{\mathbf{G}\mathbf{a}\mathbf{u}\mathbf{s}\mathbf{s}\mathbf{i}\mathbf{a}\mathbf{n}\mathbf{ }\mathbf{surface}}{\mathbf{\oint }}\mathit{d}\mathit{A}\mathbf{=}\frac{\mathit{Q}}{{\mathit{ϵ}}_{\mathit{o}}}$                

3. $\mathbf{\oint }\mathit{d}\mathit{A}$ = total   area   of  Gaussian   surface  =  4π r²  

                 Gaussian Surface

4. E.4 π r² =  $\frac{\mathit{Q}}{{\mathit{ϵ}}_{\mathit{o}}}$

5. $\mathit{E}\mathbf{=}\frac{\mathbf{1}}{\mathbf{4}\mathit{\pi }{\mathit{ϵ}}_{\mathit{o}}}\frac{\mathit{Q}}{{\mathit{r}}^{\mathbf{2}}}$    

6.  In   vector  form, $\overrightarrow{\mathit{E}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{4}\mathit{\pi }{\mathit{ϵ}}_{\mathit{o}}}\frac{\mathit{Q}}{{\mathit{r}}^{\mathbf{2}}}\widehat{\mathit{r}}$

7. The electric field must point radially outward if  Q  >  0   and   radially inward if  Q  <  0.

Case ii :  At a point on the surface of the spherical shell  (r  =  R)

$\overrightarrow{\mathit{E}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{4}\mathit{\pi }{\mathit{ϵ}}_{\mathit{o}}}\frac{\mathit{Q}}{{\mathit{R}}^{\mathbf{2}}}\widehat{\mathit{r}}$ The electric field at points on the  spherical shell (r  =  R) is given by

Case iii :  At a point inside  the spherical shell  (r  <  R)

For point outside the spherical shell , a spherical Gaussian surface smaller than the spherical shell  1. Consider a point P  inside the shell at a distance r from the centre. A Gaussian sphere of radius r is constructed .

2. Applying Gauss law: $\underset{\mathbf{G}\mathbf{a}\mathbf{u}\mathbf{s}\mathbf{s}\mathbf{i}\mathbf{a}\mathbf{n}\mathbf{ }\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{f}\mathbf{a}\mathbf{c}\mathbf{e}}{\mathbf{\oint }}\overrightarrow{\mathbf{ E}}\mathbf{.}\mathbf{d}\overrightarrow{\mathbf{A}}\mathbf{=}\frac{\mathbf{Q}}{{\mathbf{ϵ}}_{\mathbf{o}}}$     

3. $\mathit{E}\mathbf{.}\mathbf{4}\mathit{\pi }{\mathit{r}}^{\mathbf{2}}\mathbf{=}\frac{\mathbf{Q}}{{\mathbf{ϵ}}_{\mathbf{o}}}$ 

4. Gaussian surface encloses no charge,  Q  =  0   then   E  =  0    (r  <  R)

5. Electric field due to the uniformly charged spherical shell is zero at all points inside the  shell.   

 

 14. Discuss the various properties of conductors in electrostatic equilibrium.

(i) Electric field is zero everywhere inside the conductor whether the conductor is solid or hollow.   

1. If electric field is not zero inside the metal , there will be force on mobile charge.

2. There will be net motion of mobile charge contradicts with conductor in electrostatic equilibrium.

3. Thus electric field is zero everywhere inside the conductor.

4. Before applying external field , the free electrons in conductor are uniformly distributed.

5. After applying external field , left plate be negatively charged , right plate be positively charged.

6. Due to realignment of free electron internal electric field created inside the conductor.

7. Internal electric field nullifies the external electric field.

8. Conductor reach electrostatic equilibrium in the order of 10^-16 s.    

 

(ii) . There is no net charge inside the conductor. The charges must reside only on the surface of   the Conductors.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Consider an arbitrarily shaped conductor.                                             

 1. Gaussian surface drawn inside the conductor which is very close to conductor.

 2. Electric field is zero everywhere inside the conductor , net electric flux is also zero .

 3. From Gauss’s law , this implies that there is no net charge inside the conductor.

 4. If  some charge is introduced inside the conductor , it immediately reaches  surface of conductor.

 

 (iii). The electric field outside the conductor is perpendicular to the surface the conductor and has  magnitude  of  where σ  is the surface charge density at that point.

 1. If electric field component has  parallel to surface of conductor , then the free electron on the   surface       of the conductor experience acceleration . Then conductor is not in equilibrium.

 2. At electrostatic equilibrium , the electric field will be perpendicular to conductor surface.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Electric field is normal to the surface of the conductor.           

Consider small cylindrical Gaussian surface, one half of this cylinder is embedded inside conductor.                            

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Curved part: Electric flux is zero.
Bottom part: Electric flux is zero.
Top part: Electric flux is not  zero.

 

 

IV. Exercises.    

Physics